Notes¶

To do¶

Notes about files¶

The FiniteVoume11bck is a newer version of the FiniteVoume11. The new version has a different initialization, and creates a file called startparam.mat.

IDZFunDist is used by the file model comparison. (f)

Notes about SV¶

To fix¶

How to determine the simulation length for hte initialisation???

Initialisation

what happens when UseInitialisation is zero?

Describe the ini file

Check also for the files for Jeroen the system size issues, so that it works for one size.

Group the functions to a separate folder. Make clear about all files what they do.

Only the file b_channeltype11 uses the FiniteVoume11 file, all the others are using the bck file. The differences should be analyzed. Note that the finitevoume11 file, before I start messing up it today, was modified 05/24/2017. While the back was modified 07/03/2017

%UseInitialization - it is zero if we ininitalize % - it is 1 when we use an initialization % - it is 2 when we create one, it is an initialisation % run % - if it is 3, we load a file with initial values that we % created when it was less than 3

0: an initialisation based on steady state profile is calculated 1: use given time series for initialisation 2: an initialisation based on steady state profile is calculated, H downstream 3: loading created parameters

if UseInitialization==2: DischargeDownstreamBoundary=0;
else: DischargeDownstreamBoundary=1;

end

if UseInitialization<3

if UseInitialization==1

H=HinitGiven; HinitH=HinitGiven;

else (0 or 2)

H=HinitH;

end

else: load startparam HinitH=1;

end

if UseInitialization<3 save startparam Qt Ksi Hf Q Uf H Af ch end

First, establish the equivalence between the two files. The bck with zero should be the same as the 11 without bck.

Compatiblity

If anywhere you find a Voume11 wihtout bck, it is the same, if bck has the two last parameters zero. Take into account that the new has by default 1 prof factor.

Quotation from Litrico’s book¶

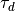The backwater area A_d gives the magnitude of the frequency respose of hte sytem for low frequencies, and the time delay $\tau_{d}$ is essential to idnetify the limits of performance of hte system, i.e. the maximum achievalbe frequency 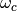$\omega_{c}$ where perturbations can be rejected. This freqency can be estimated by 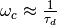$\omega_{c} \approx \frac{1}{\tau_{d}}$ (Aström 2000; Litrico and Fromion 2001). This is hte best achievable real-time performnace of the contolled system; it is not possible to reject perturbations of freqency higher than $\omega_{c}$ with distand downstream feedback control. This is a structural limitation, because it applies for any linear controller.

Backwater todo¶

Check if the areas are linearly related and if not try to figure out… or leave it. But.
make the program faster by setting the right frequecny. One would not be enough???
compare it to inertial
Make the file f_ModelComparisonArticle ok. Include the simple bw in it. Make more examples
Check and finalize the ID area and the IDZ parameter calculation functions
idz distributed
analyze the bode plots of trapezoidal and rectangular
test the approximations on trapezoidal and rectangular
Describe alpha, kappa, gamma
Document getting Bode information for the middle and test
Make a separate backwater area calculation, and call it from all the functions
write nicely the backwater area computation
make the two examples to show what it can and what it cannot, use also SV computation
if you have a lot of time: compare SV chezy and manning with the step. Does the final value depend on those?
try to make thus the SV manning.
after having all the files, it would be nice if you could make a complete comparison using csv input
write IR clearly down, implement the shift

General todo¶

finish the model function documentation
Try to make the old simhydro files run
Especially make a simhydro folder
get back the ability for Sobek scripting

Joris paper todo¶

Make a study and understanding about upstream bodes
Make a connection between categories and normal flow
Revise linear inertial
Based on this, review Hayami, also how distributed they are
Based on this, review id, also how distributed they are
Based on this, review idr, also how distributed they are
code the IR found shift
check linear inertial model
make ir distributed, document it

For backwater article¶

Article content¶

Goal: distributed backwater approximations

Show three step responds and its reproducibility We are going to show / test different methods: - based on IDZ - based on Bode - nothing - compared to linear inertial model

Make comparisons in time and space domain, using different examples Show results with fricitonless flat canal

How to approach the middle of the reach?

Dealing with IDZ¶

For the delay it is clear.
For the backwater area I found a method that should be tested.
For the zeros?

To do Joris paper¶

order and check the files
make closed loop runs (Python or Matlab?)
make the bode plots - again!
Explain a ctr talk about peak height with bode plots, talking about the sampling time
Make a test with PID as well (start from typical tuning rules)
Write / search for my MPC algorithm

Use the categories of Joris, add IR
Use the cat. of Joris, make freq. plot
Think on Inertial how to do it
Put the closed loop - RTC tools???
Look for how to make the Bode plot analytically
Create bode from time

Publication plans¶

Publication bw area, reference Pau, reference Fatiha

To read¶

Yolanda Bolea, Vicenç Puig, and Antoni Grau. Discussion on muskingum versus integrator-delay models for control objectives.: Journal of Applied Mathematics, 2014, 2014.