Steady state profile calculation¶
How to use¶
It is a Matlab function, that can be called with the following code:
HinitH= SteadyState(L, z, B ,n, Sb ,q ,h, NodeNum, friction_coef)
where n is the Manning’s coefficient, q is the discharge, B is the bottom width, Sb is the bottom slope, Y0 is the downstream water depth and L is the length of the channel. NodeNum is the number of discretisation points. The last parameter is not compulsory, the default is Chézy. If a zero is given, than it means Manning’s roughness is used(and 1 means Chezy).
Implementation¶
Integration by Euler.
Validation¶
Manning¶
If the normal depth is calculated by Manning coefficient, then the steady state profile goes to that as well if in the calculation Manning coefficient is chosen. The steady state using Manning is going to normal depth.
Chézy¶
If the Chezy coefficient is chosen, the normal depth calculated by the program will be slightly different than the one calculated by Manning. The advantage of using Chézy coefficient is that the unsteady solver is also using that, so it is easy for initialisation purposes.
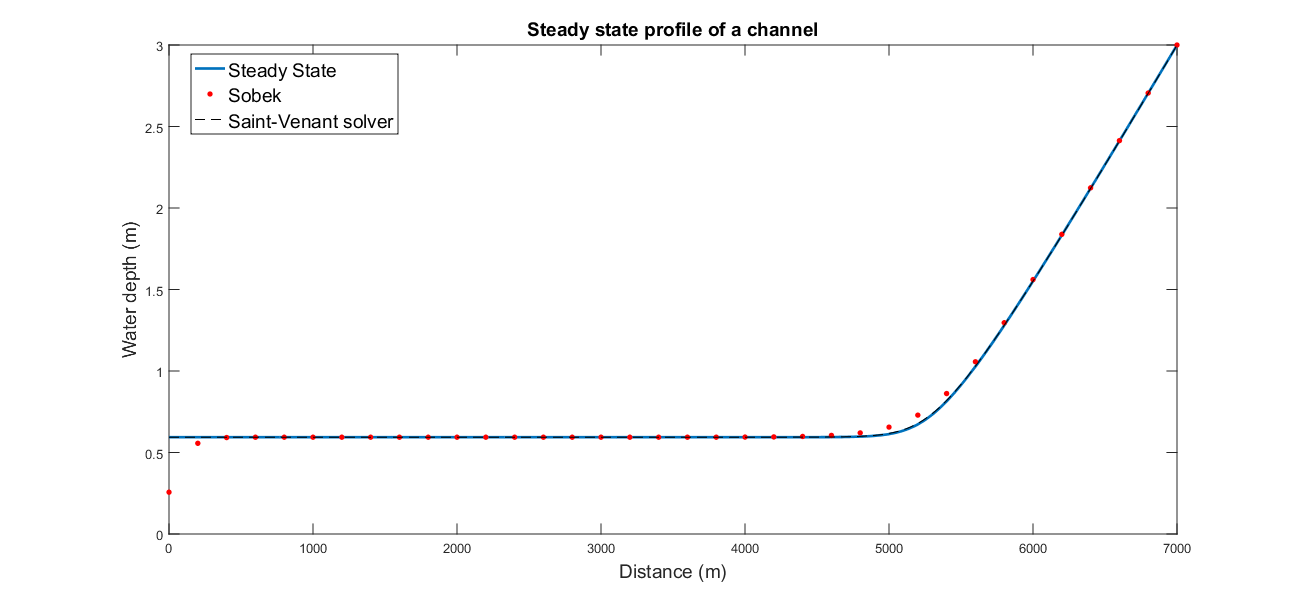
Comparison with Sobek¶
The steady state profile calculated by Sobek is compared to the one calculated by the steady state and also the result of the SV solver. The following data was used: s=0.0015; L=7000; Bw=3; z=0; n=0.03; q=1.5; h=3;
For the SV: dt=10 NodeNum=1000
The Sobek results are obtained with 200 m spatial discretisation and 5 min timestep, and 33.333 Chézy value. Note that the first two values of the Sobek results are different due to the location of water level and velocity nodes..